多臂赌博机(Multi-armed Bandits)
1.1 问题描述
强化学习和监督学习的最大区别是,对于一个动作,RL给出的是评估(evaluation),而SL给出的是判断或者说指导(instruction)。意思是说,RL通过价值函数告诉你这个动作有多好,而并不告诉你这个动作是最好的或最差的,SL正相反,他会告诉你哪个动作是正确的。当然也有一些情况,评估和指导可以联合起来训练模型,但是这里我们先用多臂赌博机来展示一下RL“给出评估”的特点,同时也展示一些最基本的RL方法。
问题是这样的,你面前有$k$台赌博机,它们之间是独立的,但不相同。在每一个时间点$t$,你的动作是选择一台赌博机$A_t$,这台赌博机会以一个概率分布给你返回一个数值奖励$R_t$,每台赌博机的概率分布不同,但不会随时间变化。在固定的时间内,比如1000个时间点内,你要获得最大奖励。
(多臂赌博机这一词的来源是多个单臂赌博机(one-armed Bandit),也就是我们说的老虎机,它有一个拉杆,拉下来就是玩一次)
图0:多臂赌博机(都找不到高清的示意图,难受)
如果每个赌博机的概率分布都知道,那其实这个问题很简单,就是每一步都选择期望最高的那个赌博机。你现在并不知道,但可以去估计,在任意时间点,你会对每个赌博机的奖励期望有一个估计值$q_{*}(a) \doteq \mathbb{E}\left[R_{t} | A_{t}=a\right]$,这个值也叫价值函数$Q_t(a)$。
如果你这个时间点的决策选取的是奖励期望最大的那个赌博机,那么这个动作叫贪心动作(greedy actions),做出这样的动作叫开发(exploiting),是在已知知识下获得最大奖励的动作。反之,如果你不做贪心动作,这个叫探索(exploring),它虽然牺牲了一部分奖励,但有助于更好地估计整个模型,或许会有利于长期的奖励。RL里一个很基本的矛盾就是开发-探索矛盾(exploting-exploring conflict)。
多臂赌博机问题里,很明显就是一个开发-探索矛盾,怎么平衡呢?一般来说,选择开发还是探索取决于几个情况:估计的精确度、剩余的不确定性和剩余的步骤。有很多相当复杂的方法,这里介绍简单的几个。
1.2 $\varepsilon-greedy$ 方法
首先,每个赌博机的价值是这么估计的
\[\begin{equation} Q_{t}(a) \doteq \frac{\text { sum of rewards when } a \text { taken prior to } t}{\text { number of times a taken prior to } t}=\frac{\sum_{i=1}^{t-1} R_{i} \cdot \mathbf{1}_{A_{i}=a}}{\sum_{i=1}^{t-1} \mathbf{1}_{A_{i}=a}} \end{equation}\]就是之前玩过这个赌博机给出的奖励求个平均啦,这其实是个很好的估计了,当选到这个赌博机的次数趋于无穷,价值函数收敛于真实奖励期望。
最简单的策略就是选择估计期望最高的一个赌博机,也就是$A_{t} \doteq \underset{a}{\arg \max } Q_{t}(a)$。但是这样的话,就没有对其他赌博机改善估计的余地了。稍微改变一下策略,以一个小的概率 $\varepsilon$ 去从所有的赌博机里随机选一个,剩下 $1-\varepsilon$ 的概率仍然使用贪心策略。这样一来,如果总的时间趋于无穷,那么每个赌博机被采样到的次数也会趋于无穷,那么对它们的估计就会是准确的。同时因为非贪心的概率很小,在探索阶段也不会对奖励的总和有太大影响。
下面两图展示了一个10臂赌博机的例子,分别用了 $\varepsilon=0$,$\varepsilon=0.1$,$\varepsilon=0.01$ 三种方法来解这个问题
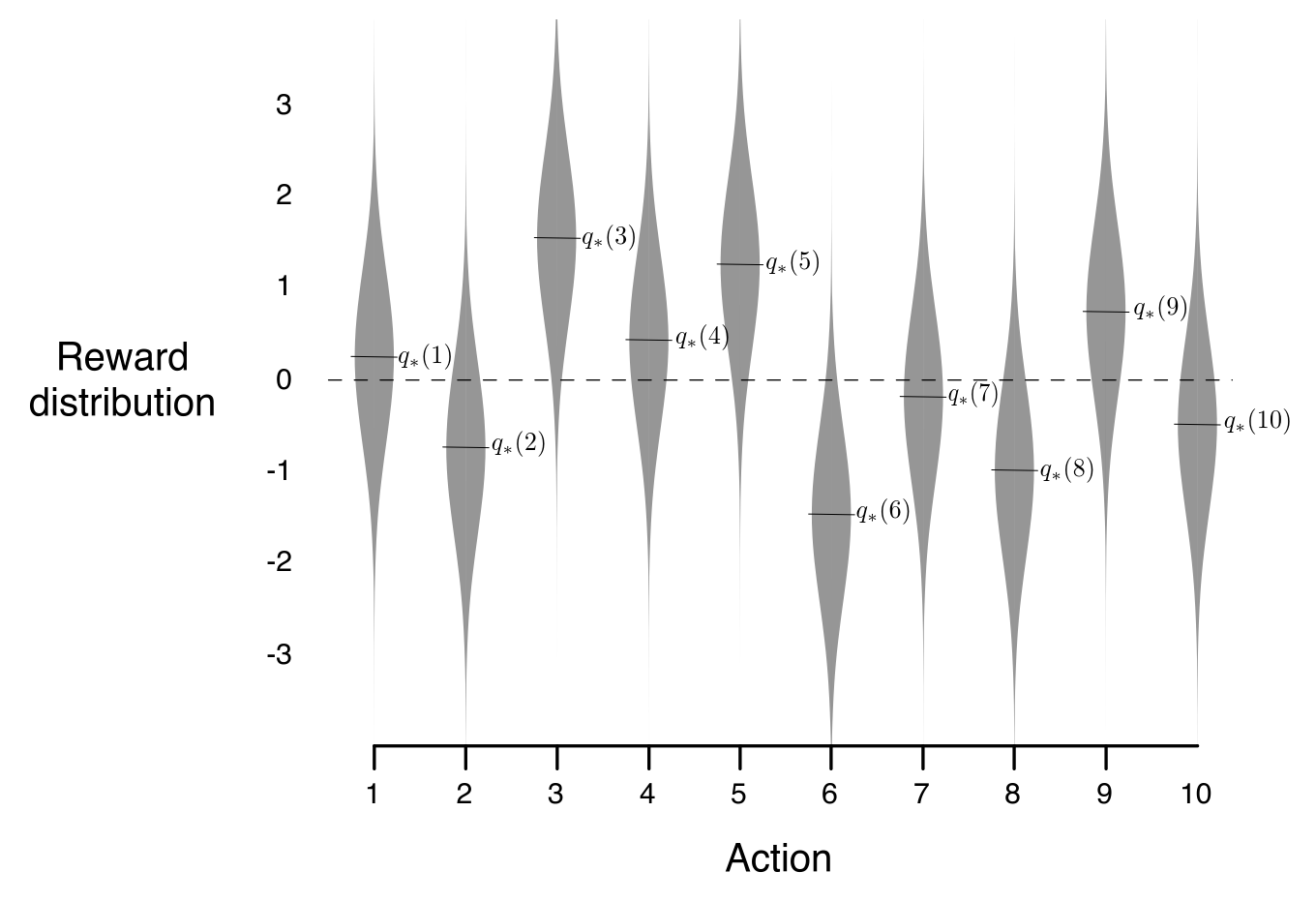
图1:上图展示的是10臂赌博机各自的概率分布和均值
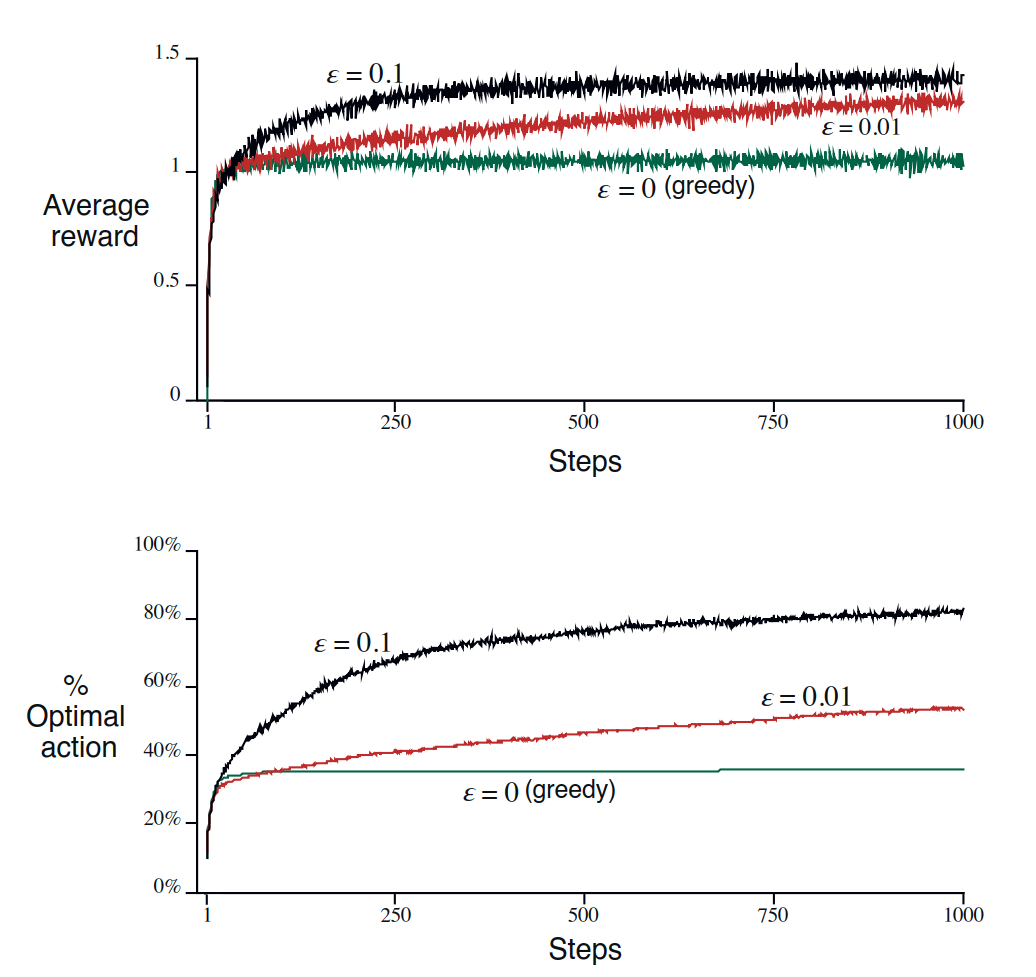
图2:上图展示的是随着时间的变化,三种方法分别会得到怎样的结果
PS:
- 如果分布的方差更大,就需要更多的探索来稳定估计
- 如果方差为0,可能贪心策略能获得更高收益,但是这些假设太强了。如果放宽一点,比如有一定的方差,或者分布不是稳定的而是会随时间改变,那么$\varepsilon-greedy$ 方法就很有优势了
- 计算均值是有增量方法的,所以并不需要每次都算个求和,增量方法能把$O(t)$的复杂度变成$O(1)$
- $\varepsilon-greedy$ 方法还是挺初值敏感的
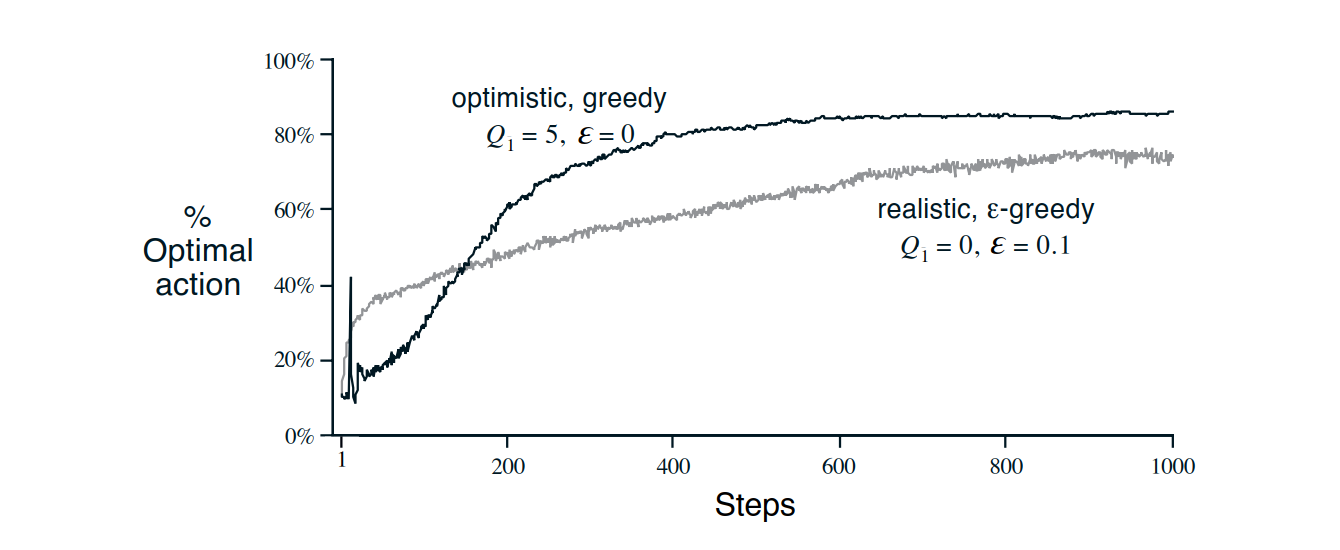
图3:上图展示了$\varepsilon-greedy$ 方法的初值敏感性——直接给出较好初值,然后用贪心算法都比较差初值的$\varepsilon-greedy$ 方法好
1.3 上置信界选择法(UCB action selection)
$\varepsilon-greedy$ 方法有一个问题,就是它无差别地对待所有的非贪心动作,但基于已有的数据,如果能对非贪心动作也有个偏好,可能能促使模型更快收敛以获得更多的奖励
一个常用的思路是使用奖励的上置信界(upper confidence bound, UCB)来选择动作,其公式是这样的
\[\begin{equation} A_{t} \doteq \underset{a}{\arg \max }\left[Q_{t}(a)+c \sqrt{\frac{\log t}{N_{t}(a)}}\right] \end{equation}\]$N_{t}(a)$ 指的是在之前的 $t$ 个时间点中,选中动作 $a$ 的次数,如果为0,就直接选取这个动作
为什么叫上置信界,简单来说,对一个均匀分布,如果采样计算均值,当采样数趋于无穷,均值会依概率收敛至分布期望。这里的“依概率收敛”就提供了一个置信区间——在某个概率下,其上界是$Q_{t}(a)+c \sqrt{\frac{\log t}{N_{t}(a)}}$。用这个上界对所有动作进行排序,选择最大的一个作为这个时间点的执行动作。
直观上来看,上置信界的公式包含两部分,$Q_{t}(a)$是确定的估计量,$\sqrt{\frac{\log t}{N_{t}(a)}}$ 是置信区间的宽度(的一半),表示不确定性的度量。我们从两个角度看不确定项会怎么变化:
- 如果一个时间点没有选到动作 $a$ ,$\log{t}$ 会增大而 $N_t(a)$ 不变,这个动作的不确定性会增大,下一个时间点会更有可能选到这个动作。反之,如果一个时间点选到了这个动作,分子分母都会增大,但对数函数增量较小,这一项整体会减小,下一个时间点就更不利于选到这个动作
- $\log{t}$ 的增速是逐渐放缓的,但没有上界,所以每个动作都会被选到,但是随着时间的增加,选到非贪心动作的频率就会逐渐变低(其实变低得很快,对数很强的),这符合我们希望在前期更多探索,在后期更多开发的直觉
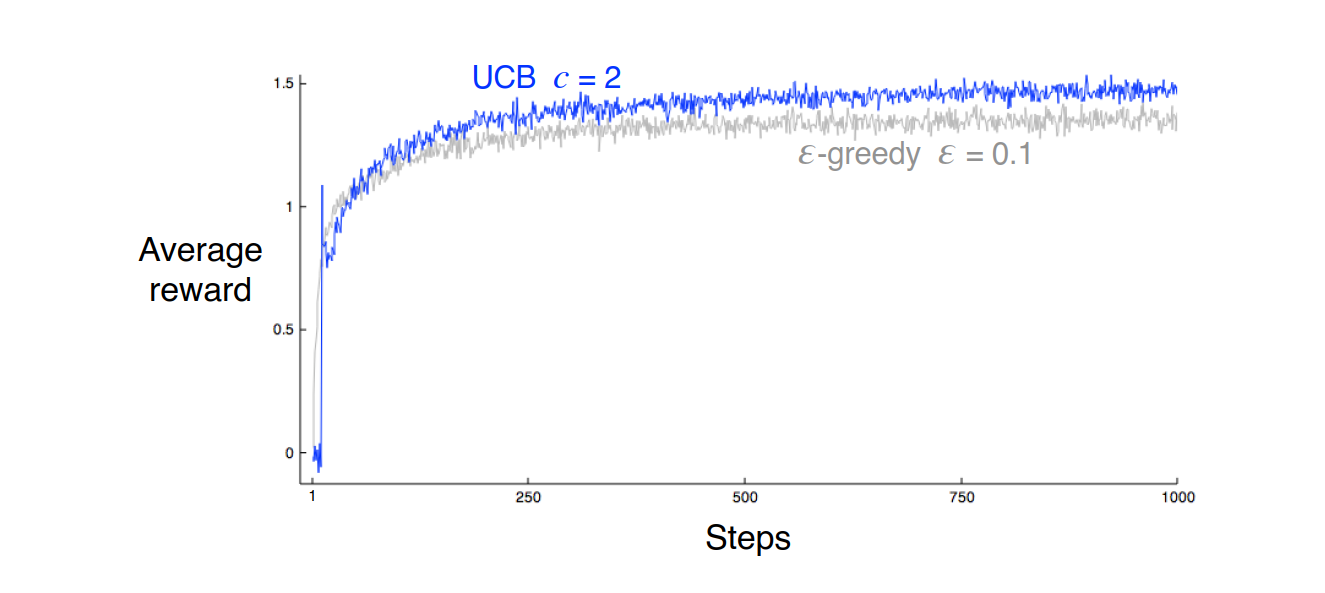
图4:多臂赌博机问题上,UCB要比$\varepsilon-greedy$ 方法好一些
PS:
- 所谓上置信界的理论解释只在均匀分布假设下成立(就是说基本不会成立),但是公式反正是什么分布都可以用,实际效果也不太依赖于均匀分布假设
- 对于多臂赌博机,UCB方法通常比$\varepsilon-greedy$ 方法效果好,但是UCB的可扩展性比较低。比如对于不稳定的分布、更多的状态空间,都不太适用
1.4 梯度方法
上面两种方法都是去估计每个动作的价值,还有另一种方法,是直接去优化策略。
把选择一个动作 $a$ 的策略 $\pi_t(a)$ 建模成一个softmax概率分布,即
\[\begin{equation} \operatorname{Pr}\left\{A_{t}=a\right\} \doteq \frac{e^{H_{t}(a)}}{\sum_{b=1}^{k} e^{H_{t}(b)}} \doteq \pi_{t}(a) \end{equation}\]这里 $H_t$ 是一些要被优化的参数,每个动作有一个参数
在一个时间点,选择一个动作 $A_t$ (并不一定要根据这个分布来采样),会得到一个奖励 $R_t$,用如下公式更新 $H_t$
\[\begin{equation} \begin{array}{ll}{H_{t+1}\left(A_{t}\right) \doteq H_{t}\left(A_{t}\right)+\alpha\left(R_{t}-\overline{R}_{t}\right)\left(1-\pi_{t}\left(A_{t}\right)\right),} & {\text { and }} \\ {H_{t+1}(a) \doteq H_{t}(a)-\alpha\left(R_{t}-\overline{R}_{t}\right) \pi_{t}(a),} & {\forall a \neq A_{t}}\end{array} \end{equation}\]其中 $\overline{R}_{t}$ 称作基线(baseline),是 $t$ 时刻所有动作得到奖励的平均。

图5:是否有baseline,以及参数 $\alpha$ 的选择对梯度方法效果的影响
1.4.1 策略梯度
这个更新公式其实就是个SGD,把它看作一个只有输入输出层的神经网络就很好理解了——输入层是状态,赌博机问题中只有一个状态,所以就一个神经元,输出恒为1;输出层是动作,k臂赌博机就是k个输出的softmax,目标函数是
\[\begin{equation} \mathbb{E}\left[R_{t}\right] \doteq \sum_{b} \pi_{t}(b) q_{*}(b) \end{equation}\]这样构造损失函数的方法叫做策略梯度(policy gradient),显而易见它由两部分组成, $\pi_t(b)$ 表示你对选择动作 $b$ 的自信程度,$q_*(b)$ 表示选择动作 $b$ 后获得的奖励——如果你很自信,结果也很好,就是一个很强的正反馈,如果不自信,反馈就会比较小,而如果自信的选择带来了很坏的结果,就必须要给很强的负反馈作为惩罚了。
1.5 几种方法的比较
四种方法的总结大概是这样:
- $\varepsilon-greedy$方法大部分时候贪心,小部分时候随机探索
- 上置信界方法是确定性的,但其机制保证了会探索到非贪心动作,而且探索频率随着时间增加逐渐放缓
- 梯度方法直接通过SGD来优化选择动作的概率模型
它们之间很难说谁好,但是既然研究多臂赌博机,就在10臂赌博机上跑跑看就知道了。每个方法都有参数,所以把参数从大到小遍历一遍,也可以看看它们随参数选择的变化趋势
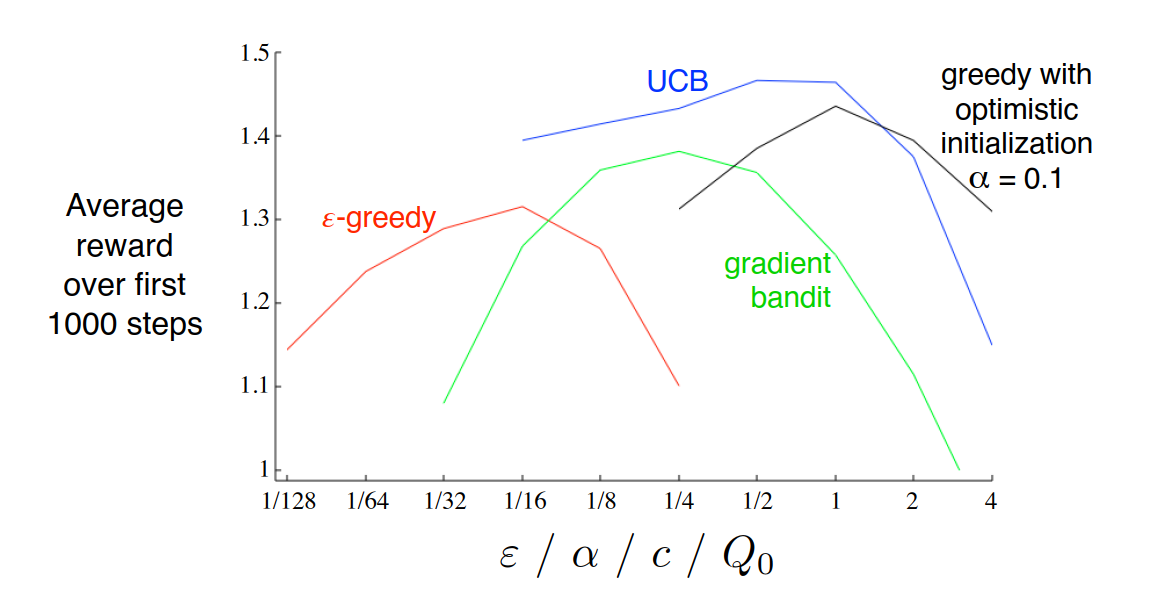
图6:三种方法,加上一个初值直接设成最优值的贪心算法,分别随各自参数的变换效果
这里很惊讶的是UCB方法居然比正确答案(最优初值的贪心)还更好,感觉很奇怪,而且贪心方法怎么还有参数也没弄明白,书里也没找到。感觉这个贪心和我理解的有一点区别,但是反正这个方法也不重要。