**1. Support Vector Machine (SVM, Logistic regression and multi class classification
1. SVM)
一个线性分类器，实际上是 $N$ 维空间上的一个 $N-1$ 维超平面。超平面将空间分成两部分，对应分类器的分类结果。如果样本空间是二维，分类器就是一条直线，如果样本是三维，分类器就是一个平面。在判别式 $y(\mathbf{x})=\mathbf{w}^{\mathrm{T}} \mathbf{x}+w_{0}$ 中，$\mathbf{w}$ 就是这个超平面的法向量，$w_{0}$ 表示超平面的平移是截距。
在上一篇文章介绍的感知机算法中，损失函数 ($E_{\mathrm{P}}(\mathbf{w})=-\sum_{n \in \mathcal{M}} \mathbf{w}^{\mathrm{T}} \boldsymbol{\phi}{n} t{n}$) 是分类错误样本的判别式之和。如果一个样本是线性可分的，则可能存在无数个超平面使得样本分类完全正确，它们对应的损失函数都是0，因此感知机算法无法再迭代更新，最后收敛于这无数超平面中的哪一个，仅取决于初值的设定。
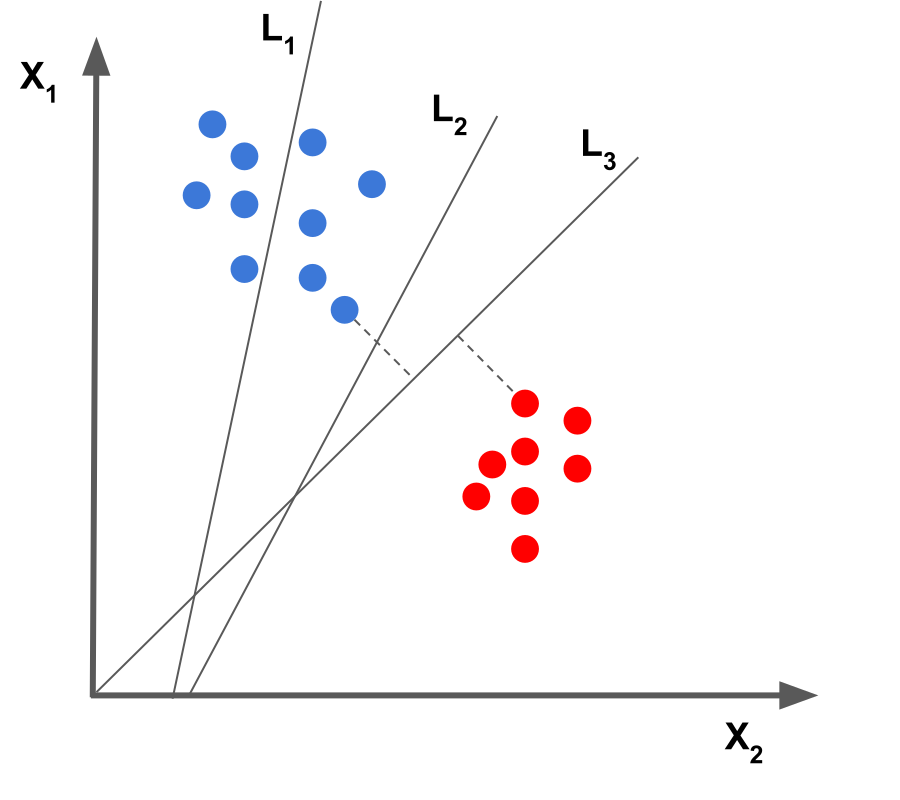$L_2, L_3$ 都是完美分类的超平面
但我们可能会想在这所有的“正确”超平面里，选出“最好”的一个。首先我们来定义“最好”：既然这些超平面在训练集上的误差都是0，没有区别，我们就考虑它们在测试集上的误差，也就是模型的泛化能力（generalization ability）。
直观上我们会认为，样本点离分类超平面越远越好，因为离得越远，样本的随机噪声带来的扰动就越不可能把样本扰动到超平面另一边去。用数学描述的话，就是离分类超平面最近的样本点，其到超平面的垂线长度要尽可能短。这个距离我们称为“边界 (margin)”，这个定义下的最优线性分类器就叫最大边界分类器 (maximum margin classifier)。
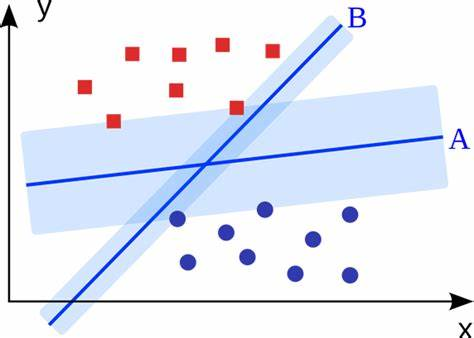比起B，很多人应该更喜欢A，因为A看起来“留有余地”
一个样本点离超平面的距离是这么算的 \(\frac{t_{n} y\left(\mathbf{x}_{n}\right)}{\|\mathbf{w}\|}=\frac{t_{n}\left(\mathbf{w}^{\mathrm{T}} \boldsymbol{\phi}\left(\mathbf{x}_{n}\right)+b\right)}{\|\mathbf{w}\|}\) 其实也就是（单位）法向量和样本向量的内积，得到样本点到过原点且平行于分类超平面的另一个平面的距离，再加上一个平移量，最后乘上$t_n$以保证距离是正值。
仔细观察发现，该式中分子分母可以同比例放缩，即 $(\mathbf{w},b)$ 变成 $K*(\mathbf{w},b)$，不会影响这个比值，这是因为法向量长度可以任取，只要垂直于超平面就行。那么固定一个优化另一个是自然而然地思路，我们可以限制法向量是一个单位向量，那么分母就会恒等于1，但在这里，我们限制分子，也就是优化下式
\[\arg \min _{\mathbf{w}, b} \frac{1}{2}\|\mathbf{w}\|^{2}\]要满足如下约束
\[t_{n}\left(\mathbf{w}^{\mathrm{T}} \phi\left(\mathbf{x}_{n}\right)+b\right) \geqslant 1, \qquad n=1, \ldots, N\]| 也就是**我们约束所有的样本点都在 $ | y | = 1$ 边界之外，求使得法向量长度最小的 $\mathbf{w}$** |
拉格朗日乘子法解这个优化问题，构造拉格朗日函数
\[L(\mathbf{w}, b, \mathbf{a})=\frac{1}{2}\|\mathbf{w}\|^{2}-\sum_{n=1}^{N} a_{n}\left\{t_{n}\left(\mathbf{w}^{\mathrm{T}} \mathbf{\phi}\left(\mathbf{x}_{n}\right)+b\right)-1\right\}\]注意，对于这个式子，我们要求其对$\mathbf{w}$ 和 $b$ 的最小值，同时要求其对$\mathbf{a}$的最大值（拉格朗日乘子法就是这么做的）。可以先求最大再求最小，也可以反过来，在参数满足Karush-Kuhn-Tucker (KKT)条件时，这两种方法会得到相同的结果。KKT条件如下
\[\begin{array}{r}{a_{n} \geqslant 0} \\ {t_{n} y\left(\mathbf{x}_{n}\right)-1 \geqslant 0} \\ {a_{n}\left\{t_{n} y\left(\mathbf{x}_{n}\right)-1\right\}=0}\end{array}\]拉格朗日函数 $L(\mathbf{w}, b, \mathbf{a})$ 对 $\mathbf{w}$ 和 $b$ 求偏导，分别等于 $0$ ，得到下面两式
\[\begin{aligned} \mathbf{w} &=\sum_{n=1}^{N} a_{n} t_{n} \boldsymbol{\phi}\left(\mathbf{x}_{n}\right) \\ 0 &=\sum_{n=1}^{N} a_{n} t_{n} \end{aligned}\]代入$L(\mathbf{w}, b, \mathbf{a})$，$\mathbf{w}$ 和 $b$ 就消掉了，转而得到
\[\widetilde{L}(\mathbf{a})=\sum_{n=1}^{N} a_{n}-\frac{1}{2} \sum_{n=1}^{N} \sum_{m=1}^{N} a_{n} a_{m} t_{n} t_{m} k\left(\mathbf{x}_{n}, \mathbf{x}_{m}\right)\]这里的 $k\left(\mathbf{x}{n}, \mathbf{x}{m}\right)$ 指的是 $\phi (\mathbf{x}{n}) \cdot \phi(\mathbf{x}{m})$ ，两个向量的内积，以后会从这里引出核函数的概念。
到这就变成了个二次规划 (quadratic programming) 问题，我们需要找到 $N$ 个拉格朗日乘子，使得 $\widetilde{L}(\mathbf{a})$ 最小，再根据 $\mathbf{w}=\sum_{n=1}^{N} a_{n} t_{n} \phi\left(\mathbf{x}{n}\right)$ 就能得到 $\mathbf{w}$ 了， 而 $b=\frac{1}{N{\mathcal{S}}} \sum_{n \in \mathcal{S}}\left(t_{n}-\sum_{m \in \mathcal{S}} a_{m} t_{m} k\left(\mathbf{x}{n}, \mathbf{x}{m}\right)\right)$。这个优化 $\mathbf{a}$ 问题叫做直接优化 $(\mathbf{w},b)$ 的对偶问题 (dual problem)，二者得到的结果是一致的（只要满足KKT条件）。说到KKT条件，我们再来看看其中的这一项 \(a_{n}\left\{t_{n} y\left(\mathbf{x}_{n}\right)-1\right\}=0\) 可以看到，两个因子相乘等于0，其中至少一个为0。如果 $t_ny(\mathbf{x}_n)-1\neq0$，则 $a_n=0$， 其与最后的 $\mathbf{w}$ 没有关系。反之$a_n\neq 0$，这个样本会贡献最后的 $\mathbf{w}$，因为$t_ny(\mathbf{x}_n)-1=0$，说明这个样本就在分类器的margin上。也就是说，只有margin上的样本才会对最后求得的超平面产生影响，这些样本我们称作支持向量 (support vectors)，因此这个方法叫做支持向量机 (support vector machine)
PS: 1. 直观上看，这个对偶变换好像很蠢，因为一开始我们只要对 $D+1$ 个参数做优化（D是样本维数），即优化 $(\mathbf{w},b)$， 而现在我们要对 $N$ 个参数做优化，一般来说 $N$ 是远大于 $D$ 的。但这个变换带来几个好处，一个是我们只需要考虑极少数的支持向量。另外，如果样本是线性不可分的，一般我们会把它们投影到高维空间，使其线性可分，这个高维空间可以是很大的有限维，甚至可以是无穷维，这时候直接优化 $(\mathbf{w},b)$ 就不现实了。而对偶问题里与样本有关的只有一项核函数$k\left(\mathbf{x}{n}, \mathbf{x}{m}\right)$，之后我们会看到，核函数的引入大大方便了这个“投影到高维”的操作。
2. 对实在不好分开的数据（比如有几个错标了label的点），为了避免这极少数的几个点毁掉整个方法，可以把硬边界变成软边界，即给越过边界的样本施以惩罚，目标函数变成 \(C \sum_{n=1}^{N} \xi_{n}+\frac{1}{2}\|\mathbf{w}\|^{2}\) 其中 $\xi_{n}$ 称作“松弛因子 (slack variables)”，是样本 $n$ 越过边界的距离，这个情况下的拉格朗日方程是
\[L(\mathbf{w}, b, \mathbf{a})=\frac{1}{2}\|\mathbf{w}\|^{2}+C \sum_{n=1}^{N} \xi_{n}-\sum_{n=1}^{N} a_{n}\left\{t_{n} y\left(\mathbf{x}_{n}\right)-1+\xi_{n}\right\}-\sum_{n=1}^{N} \mu_{n} \xi_{n}\]KKT条件变成 \(\begin{aligned} a_{n} & \geqslant 0 \\ t_{n} y\left(\mathbf{x}_{n}\right)-1+\xi_{n} & \geqslant 0 \\ a_{n}\left(t_{n} y\left(\mathbf{x}_{n}\right)-1+\xi_{n}\right) &=0 \\ \mu_{n} & \geqslant 0 \\ \xi_{n} & \geqslant 0 \\ \mu_{n} \xi_{n} &=0 \end{aligned}\)
$\widetilde{L}(\mathbf{a})$ 和 $\mathbf{w}$ 不会变化，从 $a_{n}\left(t_{n} y\left(\mathbf{x}{n}\right)-1+\xi{n}\right)$ 这个式子可以看出，结果仍然只和支持向量有关，但支持向量变成边界上的，以及越过边界的所有样本
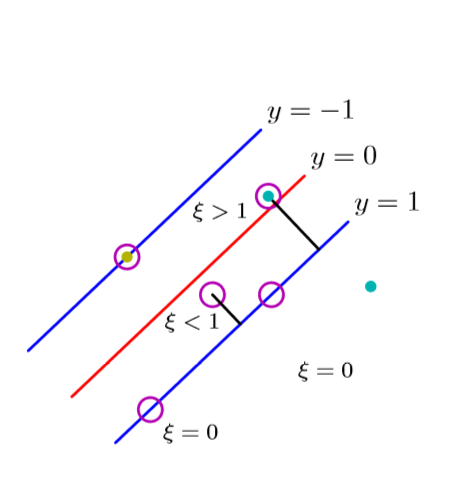允许样本越过边界的SVM，边界大小与越界惩罚的重要性用参数 $C$ 来调节