Dual Learning

link to the paper

Problem

• Neural machine translation (NMT) needs large amount data to train
• Human labeling is costly, which leads to lack of labeled data. However, unlabeded data is enormous
• How to take advantage of these unlabeled data to train a NMT model

Inspiration

• Translation is a bi-direction task. English-to-French and French-to-English are dual tasks
• Dual tasks can form a loop and get feedback from each other
• These feedback signals can be used to train the model, without a human labeler

Introduction

1. State-of-the-art machine translation methods

• Phrase-based statistical translation
• Neural networks based translation
• both heavily rely on aligned parallel training corpora

2. Neural Machine Translation

• RNN & LSTM/GRU
  • 
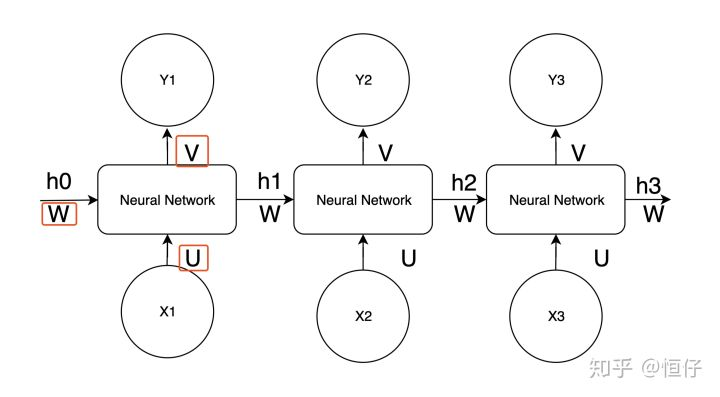
  • has problem of gradient vanish/exploding
  • if using LSTM, have problem when target sentence is longer then the source
• Seq2Seq
  • 
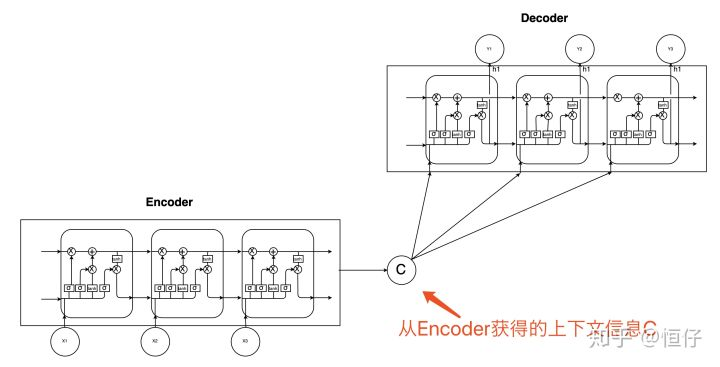
  • for $y_t$, it can use information before the time step $t$
  • if $\Theta$ is all parameters in this model, there should be:
  • \[\Theta^*=argmax_\Theta {\sum_{(x,y)\in D}\sum_{t=1}^{T_y}\log_P(y_t|y<t,x;\Theta)}\]

3. About corpora

• parallel data are usually limited in scale
• alomse unlimit monolingual data in the Web, which are used in two ways:
  • training a language model
    • is not a real address of the shortage of training data
  • generating pseudo bilingual sentences, enlarging the training set
    • no guarantee on the quality

Method

The main idea is clear: for any sentence $s_A$ in language A, first use translator $\Theta_{AB}$ to translate it to $s_{mid}$ in language B. Then language model $LM_B$ evaluate the quality of $s_{mid}$. Note that the evaluation is only linguistic instead of the meaning of the sentence. Then $s_{mid}$ is translated back to language A, which is kind of “supervised” cause we already know the original sentence.

Here we will have two parts of reward:

• $r_1$ is the language model reward, rewarding the translation from A to B, $r_1=LM_B(s_{mid})$

• $r_2$ is the communication reward, rewarding the back translation, $r_2=P(s_A

  s_{mid},\Theta_{BA})

• the final reward is just the linear combination of $r_1$ and $r_2$

Although it is intuitive to understand its idea, some of details in the algorithm may be unfamiliar to us:

• beam search

  • we want to maximize $P(s_{mid}

    s_A, \Theta_{AB})$

  • however, the target sentence comes out word by word
  • It is too costly to compute every combination of $s_{mid}$, and a strict greedy search will be likely to have a local maximum.
  • A beam search computes the joint likelihood of all combination in each time step, but only keep $K$ candidates with the largest likelihood for search afterward. This method is less computationally expensive and more unlikely to have a local maximum.
• policy gradient
  • it is not possible to gradient a sentence, since it is a discrete variable
  • in Reinforcement Learning, people use policy gradient to solve these problems

  • construct a loss function $E(a)=\Sigma_{t=1}^{end} P(a_t

    s_t,\Theta)r(a_t,s_t)$, where $s_t$ is the status in time point t, $a_t$ is the action that is taken in t. r(a_t,s_t) is the final reward, for example, wining or losing a board game

  • it come from a simple intuition: if the result is good, the action is right, and vice versa
  • in this case, $a_t$ is $s_{mid}$, subsequent derivation will be obvious

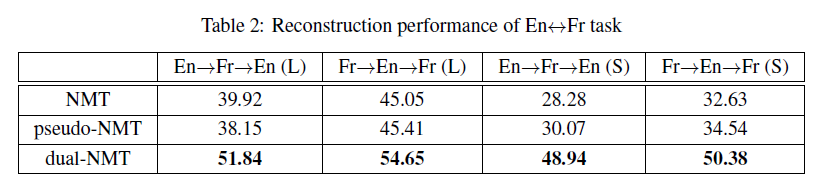
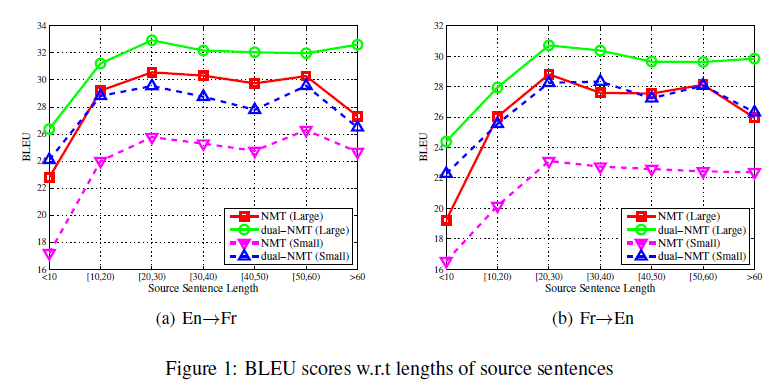
Experiment

I don’t want to talk about this part, they just claimed that they are good